Great that we got same P!
You are entirely correct, the S that I gave corresponds to the first “record position” (a position that reached further than any positions before) of the period, which (a) is not exactly S in the best case scenario (b) could in fact overestimate S in a case where the transient regime went really far. [Decider] Translated cyclers (described here, Section 3 in more details) only detects period when record positions occur, hence in a case like scribbled under, the algorithm will not recognise the period when it first occurs, but when it starts visiting unseen positions:
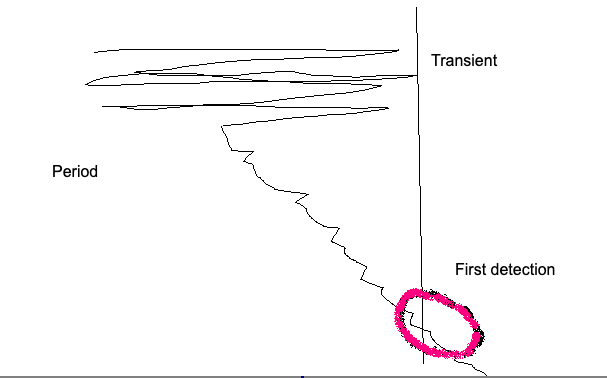
Hence, my values of S are to be ignored until I fix this.