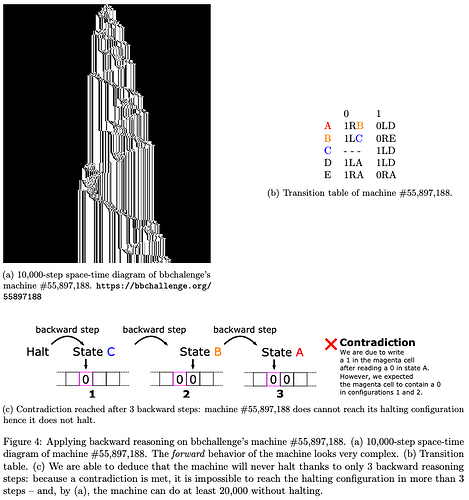
Backward reasoning: principle
This decider is not related to a specific family of the zoology.
We take the same idea of “Backward reasoning” as in Heiner Marxen - Attacking the Busy Beaver 5.
We can afford to run the decider on depth 300 (instead of 5 in Heiner Marxen - Attacking the Busy Beaver 5) thanks to having more computing power and the relatively small subset of machines on which it was run.
Click on the image below for more details about the technique:
Decider examples and counterexamples
- Examples: #4,843,748; #58,360,621; #2,009,846. More in the tests.
- Counterexamples: See tests.
Decider code
https://github.com/bbchallenge/bbchallenge-deciders/tree/main/decider-backward-reasoning
Decider tests
Results
-
09/10/22: the bug found by @TonyG was solved results of the two implementations agree (@TonyG 's and @cosmo’s) hence the decider has been re-applied officially: it decided 2,035,598 machines. To this date, there are 1,538,624 machines left to decide!
-
02/10/22: new bug found by @TonyG, the results of backward reasoning have been unapplied and now the decider must be debugged is required to pass the new [Debate & Vote] Deciders’ validation process in order to be applied. We are back to 3,574,222 machines to decide. -
27/06/2204/06/22: a bug fix was proposed for the bug outlined by @sligocki, https://github.com/bbchallenge/bbchallenge-deciders/pull/7. A bug fix was proposed for the bug outlined by @lijil. https://github.com/bbchallenge/bbchallenge-deciders/pull/8.
The decider was run up to depth 50 and decided 2,035,610 machines (among the remaining ones after [Decider] Cyclers and [Decider] Translated cyclers) of which IDs in the seed DB are available at http://docs.bbchallenge.org/bb5_decided_indexes/backward-reasoning-run-78af853d8968-depth-50-minIndex-0-maxIndex-88664064. -
13/05/22: the bug found by @modderme123 and @atticuscull has been correctedAn implementation bug was outlined by @sligocki, see Skelet #10 Backtracking?.
. The decider was applied on the index of undecided machines and it decided 2,243,340 machines available at http://docs.bbchallenge.org/bb5_decided_indexes/backward-reasoning-run-370b72380a8d-depth-300-minIndex-0-maxIndex-88664064. -
09/02/22: 1,253,418 / 3,577,204 machines were decided thanks to backward reasoning (only applied on undecided machines after cyclers and translated cyclers deciders were applied). Indices of decided machines available here: TODOSee Backtracking Bug · Issue #1 · bbchallenge/bbchallenge-deciders · GitHub
Decider correctness
Proof available at https://github.com/bbchallenge/bbchallenge-proofs/blob/build-latex-pdf/deciders/correctness-deciders.pdf.